eduroam, OpenSSL 3, and wpa_supplicant

October 3, 2022 personal

This is a story about NixOS, which is a Linux distribution based around declarative configuration. When using NixOS, instead of editing a variety of config files and installing packages one by one, the user edits a configuration.nix which describes how to generate the system.

This is not always easier, but on the whole I very much like NixOS. It’s wonderful to have a record of what I’ve done to configure my machines, to share configuration.nix across multiple machines.

And sometimes I am very impressed with how cleanly NixOS solves certain problems.

Last week, I was not able to connect to eduroam after upgrading OpenSSL. Running journalctl -u wpa_supplicant.service revealed

wpa_supplicant[2213]: SSL: SSL3 alert: write (local SSL3 detected an error):fatal:handshake failure
wpa_supplicant[2213]: OpenSSL: openssl_handshake - SSL_connect error:0A000152:SSL routines::unsafe legacy renegotiation disabled

So this seemed to be an issue with OpenSSL not supporting certain legacy protocols.

Some searching revealed that James Ralston discussed this issue and described a patch to wpa_supplicant to support legacy servers. Here’s eduroam.patch:

--- wpa_supplicant-2.10/src/crypto/tls_openssl.c	2022-01-16 15:51:29.000000000 -0500
+++ src/crypto/tls_openssl.c.legacy	2022-09-29 10:10:02.999974141 -0400
@@ -1048,7 +1048,7 @@
 
 	SSL_CTX_set_options(ssl, SSL_OP_NO_SSLv2);
 	SSL_CTX_set_options(ssl, SSL_OP_NO_SSLv3);
-
+        SSL_CTX_set_options(ssl, SSL_OP_LEGACY_SERVER_CONNECT);
 	SSL_CTX_set_mode(ssl, SSL_MODE_AUTO_RETRY);
 
 #ifdef SSL_MODE_NO_AUTO_CHAIN

This patch sets SSL_OP_LEGACY_SERVER_CONNECT which, in older versions of OpenSSL, had been set by default. From an older version of man SSL_clear_options:

The option SSL_OP_LEGACY_SERVER_CONNECT is currently set by default even though it has security implications: otherwise it would be impossible to connect to unpatched servers (i.e. all of them initially) and this is clearly not acceptable. Renegotiation is permitted because this does not add any additional security issues: during an attack clients do not see any renegotiations anyway.

As more servers become patched the option SSL_OP_LEGACY_SERVER_CONNECT will not be set by default in a future version of OpenSSL.

OpenSSL client applications wishing to ensure they can connect to unpatched servers should always set SSL_OP_LEGACY_SERVER_CONNECT

To set the SSL_OP_LEGACY_SERVER_CONNECT option in wpa_supplicant, I added the following stanza to my configuration.nix:

nixpkgs.config.packageOverrides = pkgs: rec {
  wpa_supplicant = pkgs.wpa_supplicant.overrideAttrs (attrs: {
    patches = attrs.patches ++ [ ./eduroam.patch ];
  });
};

So now when I rebuild my system (with the 2.10 version of wpa_supplicant), this patch is applied. There are other ways of dealing with this, like messing with openssl.cnf to set SSL_OP_LEGACY_SERVER_CONNECT globally, or changing how wpa_supplicant is invoked to with the environment variable OPENSSL_CONF pointing to custom configuration.

Easy cases of the volume conjecture?

November 18, 2013 mathematics

The volume conjecture relates the hyperbolic volume of a knot complement to quantum invariants of the knot. Specifically, the conjecture is that

where computes the colored Jones polynomial and . For some knots , there are nice formulas for . For instance, if is the figure eight knot, then can be written as

When and one takes the limit, this sum transforms quite nicely into the Riemann sum which computes , which is the hyperbolic volume of the figure eight knot complement.

Are there other cases in which one can verify the volume conjecture directly by finding a nice form for the colored Jones polynomial? Yamazaki-Yokota in “On the limit of the colored Jones polynomial of a non-simple link” verified, in the same direct way, the volume conjecture for a certain link with volume . I hope one could find other examples by searching for links and knots with “nice” volumes in terms of the Lobachevsky function .

From my search with SnapPy,

the link in Rolfsen’s table has volume ,
the link in Rolfsen’s table has volume , and
the knot volume .

Of course, there are lots of nonhyperbolic knots and it is hard to prove the volume conjecture even for those, in spite of the fact that their hyperbolic volume is “really nice” (namely, zero!).

Reflecting Triangles, live

February 23, 2011 personal mathematics

A while back I made some movies which began with a triangle in the plane, reflected that triangle through its three sides, reflected those triangles through their sides, and so forth. The interesting result is that for only four shapes of triangles, the resulting set of triangle vertices is discrete.

Using Raphael and a plane geometry package that I wrote, I quickly redid this visualization in Javascript; you can now move the vertices around to see the effect on the reflected triangles.

Culturomics

December 18, 2010

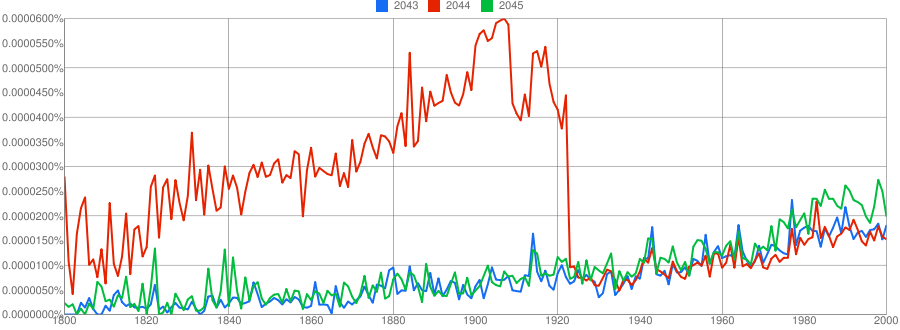
I have really fallen in love with Google Books Ngram Viewer, so I thought I’d do a little ``culturomics" myself. Here’s an image I made using Google’s data:

The brightness of the pixel at position is related to how frequently “” appears in books published in the year . Specifically, if is the number of times “” appears in print during year , divided by the number of times any number less than 2100 appears in print during that year, then is the brightness of the pixel at .

The dark, diagonal edge along the right hand side appears because in year there are many published appearances of numbers near .

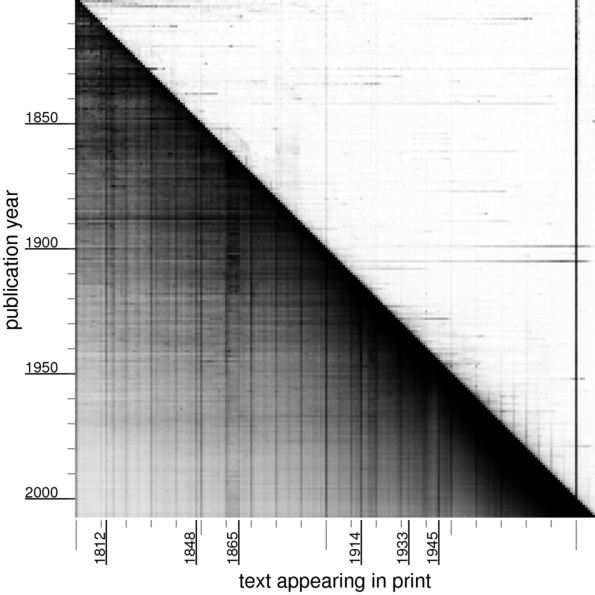
World events have left their mark on the numbers appearing in books! For example, 1914 is still being talked about long after 1914, as evidenced by the darker line above 1914.

If we look at numbers just above 1000 and turn up the contrast a bit,

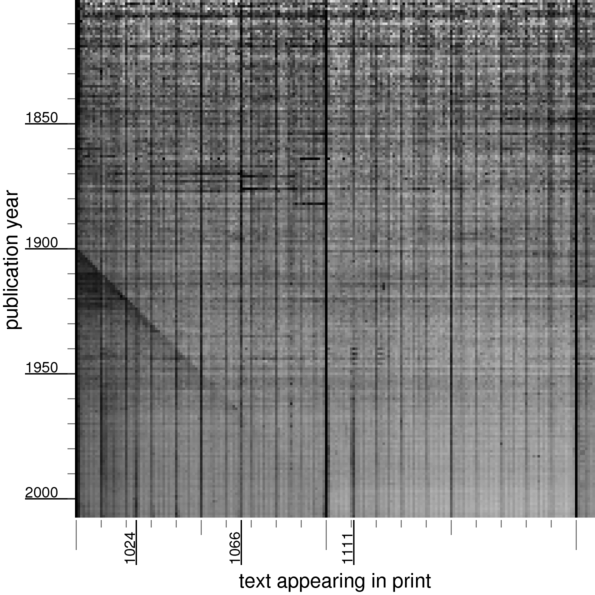
we see an echo of the dark diagonal, from people writing (or more likely, the OCR software reading) zero instead of nine in the year. There’s a dark column for the Norman conquest in 1066; a number like was not so important until the 20th century.

If we look at numbers just above 1300,

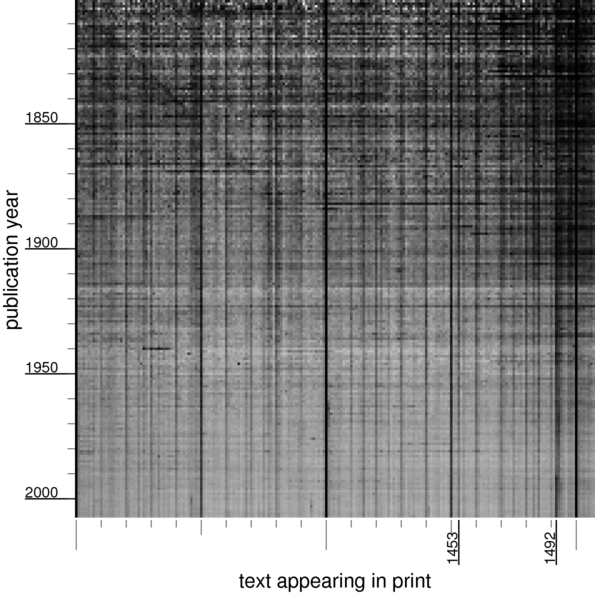
we can see an diagonal line from 1800s being read as 1300s, and a dark vertical line above 1453 (the “end” of the middle ages). In the 18th century,

1776 is quite visible. And finally, a puzzle:

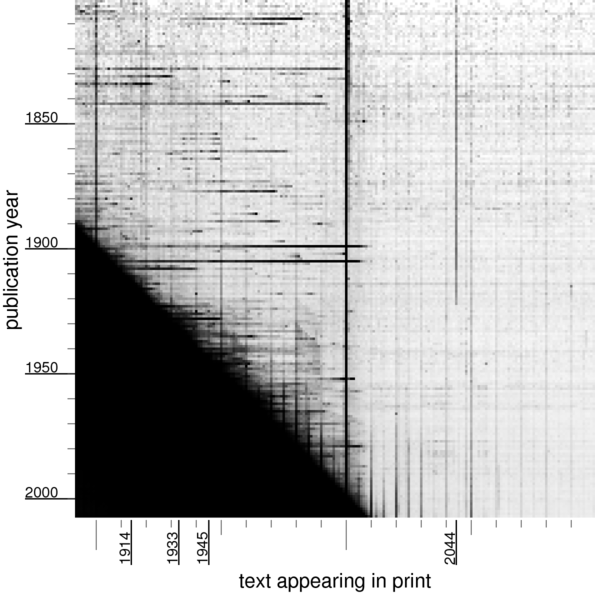
Why was “2044” so significant until the 1920s?

I’d love to know the answer to this question. The only thing I can guess that might relate the year 1919 to the year 2044 is solar eclipses.

Many more Lights Out

July 17, 2010 mathematics

A very long while ago I posted some solutions to Lights Out; back then, I solved the -by- board by row-reducing an -by- matrix.

Since then, both Boris Okun and Brent Werness pointed out to me that I should’ve solved Lights Out by using a scanning algorithm: propagating the button presses down one row at a time, and exponentiating the propagation matrix to make sure that I don’t get stuck at the last row.

This is much faster.

With this method, here is a (scaled down, auto-leveled) 2000-by-2000 solution:

And here is a (very much scaled-down, auto-leveled) 5000-by-5000 solution:

Reflecting Triangles

March 16, 2010 personal mathematics

My advisor, Shmuel Weinberger, was teaching Math 113, and asked for some pictures of the following procedure:

Start with a triangle in the plane.
Reflect that triangle across its three sides.
And repeat, reflecting the resulting triangles through their sides, and so forth.

I made a couple movies of this, illustrating this procedure as you move through the space of triangles. Observe how, for only four shapes of triangles, the resulting set of triangle vertices is discrete.