Most numbers are boring, asymptotically speaking.

 December 10, 2006 personal

\newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}}

\newenvironment{question}[1][]{\par\textbf{Question (#1).}}{} \newenvironment{theorem}[1][]{\par\textbf{Theorem (#1).}}{} \newenvironment{lemma}[1][]{\par\textbf{Lemma (#1).}}{} \newenvironment{proof}{\textit{Proof.}}{}

Let f(n) be the number of Google hits for the integer n . Then f(578) is about 100 million, and f(1156) , that is, the number of hits for a number twice as big, is about 40 million, a bit less than half as big. Doubling the input continues to halve the output: f(2312) is about 20 million (half again!), and f(4624) is about 8 million, and f(9248) is about 4 million.

There are about half as many pages talking about numbers that are twice as big. This is an example of a power law, and indeed, a log-log plot of f looks linear to my blurry vision:

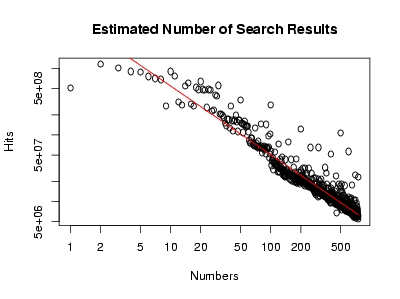
Doing a linear regression in R gives the red line, or in symbols, f(x) \approx 5,800,000,000 / x^{1.029}. Rather humorously, this means that f(a)/f(b) \approx b/a . In the end, this is not so surprising: Zipf’s law says that, in a corpus of naturally occuring text, the frequency of a word is inversely proportional to its rank; here, we have a similar phenomenon at work: roughly, the popularity of a number is inversely proportional to its size.

In other words, while the number of integers expressible with fewer than n bits grows exponentially in n , the number of pages discussing integers expressible with fewer than n bits grows linearly in n ; being silly, I’d say that this is an asymptotic version of the claim that most large numbers are uninteresting. After all, popular numbers have a lot of fan sites.