This is a story about NixOS, which is a Linux distribution based around declarative configuration. When using NixOS, instead of editing a variety of config files and installing packages one by one, the user edits a configuration.nix which describes how to generate the system.

This is not always easier, but on the whole I very much like NixOS. It’s wonderful to have a record of what I’ve done to configure my machines, to share configuration.nix across multiple machines.

And sometimes I am very impressed with how cleanly NixOS solves certain problems.

Last week, I was not able to connect to eduroam after upgrading OpenSSL. Running journalctl -u wpa_supplicant.service revealed

wpa_supplicant[2213]: SSL: SSL3 alert: write (local SSL3 detected an error):fatal:handshake failure
wpa_supplicant[2213]: OpenSSL: openssl_handshake - SSL_connect error:0A000152:SSL routines::unsafe legacy renegotiation disabled

So this seemed to be an issue with OpenSSL not supporting certain legacy protocols.

Some searching revealed that James Ralston discussed this issue and described a patch to wpa_supplicant to support legacy servers. Here’s eduroam.patch:

--- wpa_supplicant-2.10/src/crypto/tls_openssl.c	2022-01-16 15:51:29.000000000 -0500
+++ src/crypto/tls_openssl.c.legacy	2022-09-29 10:10:02.999974141 -0400
@@ -1048,7 +1048,7 @@
 
 	SSL_CTX_set_options(ssl, SSL_OP_NO_SSLv2);
 	SSL_CTX_set_options(ssl, SSL_OP_NO_SSLv3);
-
+        SSL_CTX_set_options(ssl, SSL_OP_LEGACY_SERVER_CONNECT);
 	SSL_CTX_set_mode(ssl, SSL_MODE_AUTO_RETRY);
 
 #ifdef SSL_MODE_NO_AUTO_CHAIN

This patch sets SSL_OP_LEGACY_SERVER_CONNECT which, in older versions of OpenSSL, had been set by default. From an older version of man SSL_clear_options:

The option SSL_OP_LEGACY_SERVER_CONNECT is currently set by default even though it has security implications: otherwise it would be impossible to connect to unpatched servers (i.e. all of them initially) and this is clearly not acceptable. Renegotiation is permitted because this does not add any additional security issues: during an attack clients do not see any renegotiations anyway.

As more servers become patched the option SSL_OP_LEGACY_SERVER_CONNECT will not be set by default in a future version of OpenSSL.

OpenSSL client applications wishing to ensure they can connect to unpatched servers should always set SSL_OP_LEGACY_SERVER_CONNECT

To set the SSL_OP_LEGACY_SERVER_CONNECT option in wpa_supplicant, I added the following stanza to my configuration.nix:

nixpkgs.config.packageOverrides = pkgs: rec {
  wpa_supplicant = pkgs.wpa_supplicant.overrideAttrs (attrs: {
    patches = attrs.patches ++ [ ./eduroam.patch ];
  });
};

So now when I rebuild my system (with the 2.10 version of wpa_supplicant), this patch is applied. There are other ways of dealing with this, like messing with openssl.cnf to set SSL_OP_LEGACY_SERVER_CONNECT globally, or changing how wpa_supplicant is invoked to with the environment variable OPENSSL_CONF pointing to custom configuration.

I took my road test this morning—and I passed!

After all these years, I am a licensed driver. Now, where should I drive to?

Google Trends plots the search volume (or some other measure? search percentage?) for a given phrase over time. It’s ridiculously fun!

As an example, let’s look at the number of times people search for the words hot and cold. I downloaded the CSV file offered by Google trends to make the following graph:

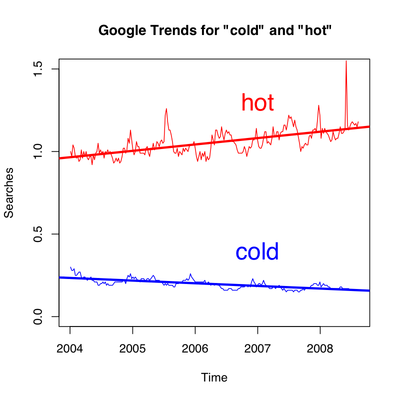
The thick red and blue lines are the linear regressions on the number of searches for hot and cold, respectively. Behold!—people are searching more often for hot lately, and less often as of late for cold! The search volume does seem to be related to the temperature: you might notice that the search volume for cold dips under the regression line during the summer, but exceeds it during the winter.

And so, global warming is being revealed in our search habits. Maybe I should’ve titled this post “Google warming.”

The Romans (among others!) wrote in wax with a stylus; the wax was embedded in boards, which were bound together in pairs. If a Roman were to place clay between these boards, could they make a copy of their wax tablet in the clay?

It strikes me as remarkable that coins were minted so long before books were printed—though I guess the motivation behind minting coins and printing books are rather different.

Drew Hevle raises a very interesting question: suppose you are stranded on a desert island; what books would be entirely useless in this situation?

Here are a few books that I wouldn’t want to be stranded on an island with:

• Federal Income Tax: Code and Regulations Selected Sections
• A Million Random Digits with 100,000 Normal Deviates
• Government Phone Book USA 2000
• How to Build an Igloo: And Other Snow Shelters

Do you have other ideas for awful desert island reading?

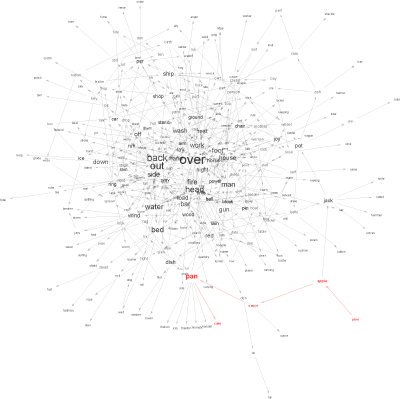
The pineapple sauce pancake graph has English words as vertices, and a directed edge from to if the concatenation is also an English word. For instance, there is a vertex labeled pine, and a vertex labeled apple, and an edge from pine to apple.

Anyway, the graph is huge; and the usual visualization tool (Graphviz) doesn’t work particularly well on the whole graph, so I took a few hundred vertices around pine, apple, sauce, pan, and cake. The result was the following:

While we (meaning my wife and I) were filling out the forms for our marriage license, we were interviewed by NPR for Morning Edition! A copy of the broadcast is available online.

National Bingo Night (which seems to me to be very silly, but ignoring that…) has a “play along at home” game, where you print out a bingo card.

How would I design this? I had hoped that the website generated a Bingo card, digitally signed it, and then sent the signed card to the user. If it had been designed that way, ABC wouldn’t even need to remember which cards had been generated, as long as their private key wasn’t compromised.

How many Bingo cards are there? The first two and last two columns of a Bingo card are a sequence of 5 numbers drawn from 15 possible numbers, and the middle column has a “free” square, so it consists of only 4 numbers from 15 possible numbers. Anyway, this is , which is a big number. In base 36, it is 18 digits long.

But the base 36 number below the National Bingo Night cards is only 10 digits long. Thus, this 10 digit number can’t encode the whole Bingo card–there are too many cards.

The official rules make this totally clear:

“ABC’s National Bingo Night” (the “Show”) Home Viewer Sweepstakes (June 2007) (the “Sweepstakes”) is a seeded instant win game. Unlike bingo, where selected numbers are drawn live before an audience of players who have purchased or otherwise obtained randomized cards, in this Sweepstakes the relevant numbers are known to Sponsor ahead of time, due to the nature of the recording schedule of the Show. Based upon the numbers drawn during prior in-studio tapings of the Show, Sponsor then randomly distributes a specific, predetermined number of potentially winning Sweepstakes “Game Cards.”

So they already know who will win, because the numbers have already been drawn. The serial number only has to encode “Winner” and “Loser.” Not so interesting.

I wonder, though, if there are other web games that actually use digitally signed objects for fun purposes?

I am frequently amazed to discover that songs which I had believed to have been original are actually covers. It turns out, for instance, that TMBG’s “Istanbul (not Constantinople)” is a cover of a song from the 1950s.

Ironically, one might argue that Istanbul is itself a cover of Constantinople–and that argument (unifying form and content) reminds me of the language games played by Salt: Grain of Life, a book asserting that its very structure resembles the culinary crystal it purports to discuss.

Most mammals produce their own vitamin C, but humans carry a mutated form of the gene responsible for one of four enzymes enzymes necessary for vitamin C production, and so we humans must find it in our diets. In effect, every human being has a metabolic deficiency!

And in light of this wonderful news, why not ingest tremendously huge amounts of vitamin C?

In fact, I’d like to make this into a double-blind study of myself. Here is what I would like to do: randomly take either a placebo pill or a vitamin C pill (without my knowing which I took), and record the type of pill I took. At the end of the day, I would further record how I feel (as a number from 1 to 100, perhaps), and then do a regression to see if the type of pill I am taking is correlated with how I feel.

In fact, I should do this with all sorts of things in my life. Certainly I should be doing this with my caffeine intake, because I feel so convinced that I am much happier while drinking coffee, but that may only be an effect of the coffee–which is, wonderfully and exactly, the point.

The question is: how little can I spend to feed myself for one week? I ought to eat 2000 calories/day, so I’ll need to purchase 14,000 calories/week.

Here’s a “healthy” option: just eat apples. One ounce of apple has 15 calories, so I’ll need to eat 58 pounds of apples per week; I might be able to get this many apples for 29 dollars.

But I can do better! One “Take 5” candy bar is delicious and contains 210 calories, so I’ll need to eat 66 candy bars per week; in the best of all possible worlds, I might be able to purchase this many candy bars for 22 dollars.

I could buy a pound of mayonnaise for two dollars. Apparently a pound of mayonnaise has 3200 calories, so I could get more than enough calories for just ten dollars a week.

Presumably I could do significantly better with potatoes or with rice?

Tasha the Cat received a new toy–a plastic circle containing corrugated cardboard, with a ball stuck in a track. Watch her pounce!

Today, I was about to sit down and read a paper (in French–I may not speak in tongues, but apparently I can read in tongues, so to speak!), and I thought to myself about how nice it would be to have a cookie. I went to Uncle Joe’s, I went to the Classics Cafe, I went to Cobb’s coffee shop, and then I gave up, for there were no cookies in any of those places, places which so often appear to be the source of cookies.

Is there someplace else on campus that I should have looked? Admittedly, I probably would’ve settled for the biscotti in the divinity school cafe (especially with some coffee).

While on public transportation, my mind wanders… And one might assume the following about me and my buses,

• The bus travels for one unit of time,
• I will get on the bus at a random time (uniformly distributed),
• I will leave the bus at a random time (independent, unformly distributed).

Then the probability that I am on the bus at time is . So one might expect that the total number of people on the bus at time to look like for some .

I would enjoy riding a bus from the start to the end, and seeing how accurate this is, though tragically, I rather doubt it is very accurate at all. For starters, the entrance and exit times are correlated (who gets off the bus one stop after they get on?), and there are places where people are more likely to enter, and where people are more likely to exit. In fact, upon further reflection, this is a horrible model of bus ridership.

But, if you, say, averaged all the bus routes to make the entrance and exit distributions more uniform…–is there anywhere I can get this data? Wait, wait, this seems like an awful idea: I’d better stop now.

Thanks to Bryce Johnson for pointing out a mistake in my calculation of the probability above–I had forgotten to include a factor of two!

When I walk down the street, I create patterns in how I walk, often by controlling my stride length so I will step on cracks every third sidewalk square, or whatnot. If I were a true master, my stride length would be incommensurable with respect to the sidewalk length–surely this was the problem that forced irrationalities upon the Greeks…

Anyway, I was also happy to realize (at a recent retreat) that clothing is nicely categorized by how many disks must be removed from a sphere to produce the particular clothing item. For some examples, consider:

• A sock or a hat is a sphere minus a disk.
• A headband (or tube top) is a sphere minus two disks.
• Jeans are a sphere minus three disks (the fabled “pair of pants”).
• A shirt is a sphere minus four disks (the “lantern”).
• A bathing suit is a sphere minus five disks.
• A fingerless glove might be a sphere minus six disks.
• Two fingerless gloves connected by a band is a sphere minus 11 disks.

Another lovely example is that of some scarves, which are a projective plane minus a disk (i.e., a Mobius strip), and therefore sit flat against one’s neck. I would be very interested in owning more non-orientable clothing (someone, somewhere, must own a non-orientable tank top–though perhaps that mythical object would be too annoying to be allowed to exist).

I’ve been (not surprisingly) drinking quite a bit of coffee lately, and I’ve noticed that many corregated coffee cup holders include a bit of loose glue. At first, I thought this was a mistake, an oversight in the perfection of the coffee cup holder design.

On the contrary, that bit of excess glue melts when the hot coffee is poured into the cup, adhering the corregated holder to the cup–brilliant!

Let be the number of Google hits for the integer . Then is about 100 million, and , that is, the number of hits for a number twice as big, is about 40 million, a bit less than half as big. Doubling the input continues to halve the output: is about 20 million (half again!), and is about 8 million, and is about 4 million.

There are about half as many pages talking about numbers that are twice as big. This is an example of a power law, and indeed, a log-log plot of looks linear to my blurry vision:

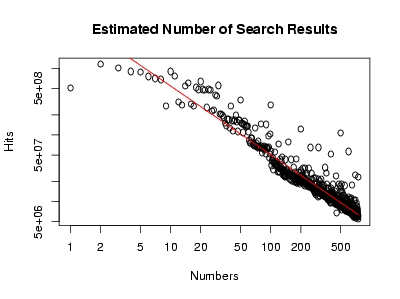
Doing a linear regression in R gives the red line, or in symbols, Rather humorously, this means that . In the end, this is not so surprising: Zipf’s law says that, in a corpus of naturally occuring text, the frequency of a word is inversely proportional to its rank; here, we have a similar phenomenon at work: roughly, the popularity of a number is inversely proportional to its size.

In other words, while the number of integers expressible with fewer than bits grows exponentially in , the number of pages discussing integers expressible with fewer than bits grows linearly in ; being silly, I’d say that this is an asymptotic version of the claim that most large numbers are uninteresting. After all, popular numbers have a lot of fan sites.

I searched for each number between 1 and 500 on Google, and recorded the (estimated) number of hits. I’m not aware of anyone having done this before; in any case, I made a chart:

Click on the above chart to see a bigger version. You can also look more closely at the first hundred numbers, or look at the above data with a log scale on the y-axis.

I have some observations and questions:

• There’s some periodicity in the above data (every 5, every 10, every 100).
• Can you explain how quickly the distribution falls off (is it exponentially decaying, for instance)?
• The most popular numbers are, in decreasing order of popularity: 2, 3, 10, 4, 5, 11, 6, 7, 8, 20, 15, 30, 14, 18, 1, 24, 21, 19, 25, 22, 28, 29, 50, and so on.
• The most popular numbers ending in 0 are, in decreasing order of popularity and having been divided by ten: 1, 2, 3, 5, 10, 4, 8, 9, 7, 20, 6, 50, 15, 12, 30, 25, 11, 40, 13, 18, 16, 14, and so on. Is the distribution of numbers ending in 0 related to the distribution of all numbers?
• Are certain families of numbers more popular? Are prime numbers or square numbers particularly popular?

You can download my comma-separated data file if you would like to play with the data yourself. Note, however, that I got this data from Google’s SOAP interface, which, for reasons I don’t understand, doesn’t give the same number of “estimated hits” as the web page interface.

What can be said about the history of static electricity? Did Greek science know about it? Any medieval experiments with static electricity?

It’s sort of interesting that people knew about magnetism and electricity for hundreds of years before finding many good uses for that knowledge (granted, compasses and potentially batteries for electroplating, but these things are trinkets in our modern world so dependent on electricity); in contrast, the span between radiation and harnessing nuclear power was much shorter (although maybe our modern uses of nuclear power will seem like mere trinkets compared to the awesome uses to come). I guess this isn’t surprising—eh, nothing I say is surprising!

And after listening to Sufjan Stevens’ “A Good Man is Hard to Find,” I read the short story with the same title. I find myself liking “Seven Swans” more and more, and the short story by Flannery O’Connor was quite interesting. The short story of the crane wife (which is used to good effect on the Decemberists new album of the same name) is quite beautiful, too.

And last night, while doing some mathematics, I was also listening to an audiobook (well, podcast) rendition of Plato’s Republic; I had forgotten the thing about the ring that turned people invisible! It’s funny enough that this gets picked up in the Lord of the Rings, but just the idea of such a ring is so provocative—where did the idea come from?

And earlier this week, I was reading about king David’s “mighty men” and about the beautiful Abishag. I find it amusing how the names of these people (e.g., Glaucon in The Republic or Abishag) get remembered, with fame far beyond their expectation, I’m sure.

I tried making bread, but with significantly less flour than neccessary (and therefore, far more water than needed). The result was very much like cooked paste. It was pointed out to me that since the essence of bread is flour, trying to get by with less flour was undermining the very essence of bread (and I find such arguments very satisfying).

I also made baklava again, and that turned out much better than the first time (which involved the baklava burning).

Sometimes I’m scared that, at some point in my past, I opened a pair of parentheses without closing them. Even worse, I’m sure I’ve feared this very thing in the past.

Then again, maybe this is the common fear of all schemers: that our whole lives might now be a parenthetical comment.

Perhaps a half-dozen times in the past week, I’ve read sentences with contain the phrase “must needs.” I have never considered this construction before; frankly, it sounds totally bizarre to my inner ear (my spiritual inner ear, that is).

Thus, it must needs be that I’ve been teleported to another world, a world in which the English language developed differently than it did in the world from which I came. This tiny grammatical gem is the only evidence of my true origin.

I’m still trying to find (two!) new roommates (since my current roommate bought a place, and is moving out on December 15th). If you know anybody who would like to move in with me, I’d love to know about it.

There are some pictures of my home.

I wonder if anyone knows about alphabet songs in other languages? I’d be particularly interested in knowing about Greek and Hebrew alphabet songs, and a bit about the history of such things. It seems like these songs must be used primarily to teach the lexicographic ordering of the letters; I suppose the Latin alphabet is ordered in keeping with the Greek alphabet, and so forth, but why did the early alphabets get placed in the order that they did? Saying “numeric value”just begs the question (after all, then why those values?).

It also seems a bit odd that Twinkle Twinkle Little Star is song for the alphabet. It also seems like the alphabet song should be related to the zed/zee distinction.

And not too surprisingly, Wikipedia has an article about the Alphabet Song. Wikipedia knows too much (although they are still missing an article about superrigidity!).

I’m fond of the Pineapple Sauce Pancake graph: the vertices are English words, and there is an edge from to if is also an English word (e.g., “pan” and “cake” are English words, and there is an edge from “pan” to “cake” because “pancake” is also an English word).

To play around with this, I wrote a Javascript program, complete with a Web 2.0 logo–which reminds me, I wonder if there is an interpreter for the programming language logo, written in Javascript?

Anyway, what I really wanted to do was to make a wall-sized picture of the Pineapple Graph, but Graphviz isn’t quite able to handle it, but maybe with some tweaking, I’d be able to produce a beautiful poster.

I’ve spent a lot of time constructing languages (Kisonef and Naedari being my favorites); in a similar vein, I also tried to create a language that an alien civilization would be able to understand. I had hoped to put a message written in my universal language in a conspicuous place (say, on a college campus), just to test if what I made really was understandable, even to humans!

But I never got around to that, and plenty of other people have done exactly that. This is related to the following question: state and prove a theorem in such a way that an alien would be able to follow your proof.

But whoa! I found out that Freudenthal (the mathematician) did the same thing: he created LINCOS. Bizarre. I also enjoyed looking at this image that we sent into space and trying to imagine what the aliens must think of people who write with such strange characters.

Last night, there was a terrible thunderstorm in Chicago; I’ve never seen so many trees on the road! I was supposed to land at Midway at 7:30pm last night, but we were diverted to Indianapolis, so I didn’t land in Chicago until 2:00am, and then I waited until 3:00am to get a taxi, so I didn’t get home until almost 4:00am. Crazy!

My house lost power last night, and today some places are still without power. In particular, Co-Op Market’s 53th street store was closed, merely displaying a sign “Closed No Power Mgmt.” Considering that their 47th street store shut down, and that their 55th still (?) lacks price scanners, I can only expect that this power outage is the final blow to Co-Op.

In contrast, the also-powerless-but-superior Hyde Park Produce Market was using a generator to power their cash registers (and to provide one very bright light in an otherwise dark store).

My cell phone still works, even after being dropped into water.

There is a program called PawSense for Windows which detects “cat-like” typing, and then prevents further keyboard entry.

I found some code for filtering keyboard events on Mac OS X, and I wanted to implement something similar. But this raises an interesting question: just what characterizes “cat-like” typing?

The PawSense website suggested that cat paws are very broad, and usually strike nearby keys simultaneously. Another idea is to detect “human-like” typing and then freeze the keyboard whenever non-human typing is detected (which has the useful feature of detecting a future version of cat with smaller paws).

This morning I went to the car to see if I could start it, and at least move it back and forth a bit (as I still don’t have my license). Fortunately, the car started! Unfortunately, the clutch doesn’t seem to do anything.

I am holding down the clutch while the car starts, but then I can’t shift into reverse: all I hear is gear-grinding. I can’t shift into first at all; the knob won’t even move there. With the car off, I shifted into reverse, and then started the car (okay okay, I realize now this was a truly stupid idea), but it merely lurched backward before the engine died. It’s just as if I let up on the clutch too quickly without enough gas…

I guess the clutch isn’t doing anythnig at all.

This must be a consequence of my having not driven it while I was away; the emergency brake is sort of loose feeling, the door locks are sticking, and, rather tellingly, the clutch sort of squeaks when I move it. I guess this means I will have it towed away again to be repaired again; at least the people at the transmission shop are very nice.

I really just want to learn how to drive. Someday, someday.

Two interesting things about taking a bath…

The first was, while singing in the bathtub, I hit a resonant frequency, and I wondered: what can be deduced about the shape of my bathtub (well, bathroom) from this frequency?

The second was that I heard something fall into Tasha’s water dish; thinking nothing of it, I was rather shocked (well, not literally shocked, but…) to find that it was my cell phone that had fallen into Tasha’s water. Uh oh.

And now I am trying to dry it off with a hairdryer.

Often, Tasha picks something up (say, a pen, or a lego), carries it around, and then drops it into her water bowl. I have no idea what she is thinking when she does this. On the topic of cat thoughts, the Wikipedia article on cats observes:

Some theories suggest that cats see their owners gone for long times of the day and assume they are out hunting, as they always have plenty of food available.

I desperately hope that Tasha believes that I am out hunting (mathematics?). In any case, seeing her carry the legos around answers an old question of mine: about two months ago, I noticed that lego pieces were “mysteriously” appearing in my shoes. The Wikipedia article goes on to note that:

It is thought that a cat presenting its owner with a dead animal thinks it’s ‘helping out’ by bringing home the kill.

In other news, the welcome dinner for GCF went spectacularly well; afterwards, we played Loaded Questions, and I learned that people associate tildes with me to a much stronger degree than I would have believed.

I left California far too quickly: some people that I had really wanted to see I didn’t get to see. But I got to spend a lot of time with my dad, which was excellent, and the conferences and Berkeley itself were a lot of fun.

I understand why clutching functions are called clutching functions: a automobile’s clutch transmits rotation from one object to another under the control of the driver, and a clutching function likewise glues together two different rotations under the control of the mathematician.

Having been gone for two weeks, the beautiful cat Tasha has decided that my chair is her chair.

I saw a poster that described a play as “crunchingly witty.” This seems like a very strange sort of wittiness to me.

I am still in California, and very much enjoying public transportation. Yesterday, I took AC Transit’s 65 bus (the “Euclid” bus) along an extremely (and therefore ironically) curvy road to get off the mountain of MSRI. (The “mountain of misery” belongs in a fantasy novel.)

There’s a lot of people in California I would still like to see.

Here is a really stupid question: If I have a wire (with a changing current) and I bend it around, and measure the induced current in (a finite number of) neighboring coils, can I determine anything about how I have bent the wire? Being more ridiculous, I will weave together wires to make fabric. How do the electrical properties of the fabric relate to its shape? That is, if I run current along one wire, and measure the induced current in other wires, can I deduce anything about how I have bent the fabric?

It strikes me as amusing to measure the speed of something by, say, attaching a magnet to the wheel and then seeing how quickly the magnet is moving past a coil. I wonder how sensitive this would have to be, say, to work as a bicycle speedometer.

Anyway, this is the stuff that bothers me on the bus. Right now, it is my inability to produce more examples of hyperbolic n-manifolds that is bothering me.

I’ve made it to Los Altos: I’m going to be staying with my dad, but during the next couple weeks visiting Berkeley to go to a conference, and to meet up with my advisor.

I ended up talking Route 22 on VTA, and then walking a few miles to go here, in the dark, using GPS to guide me. I was amazed that this method worked!

I guess I should warn you that I am about to reveal plot details of Dan Brown’s books.

I read Digital Fortress by Dan Brown, which was an unfortunate use of time. That book, for starters, is isomorphic to the Da Vinci Code; they are both about a female cryptologist, who gets involved with a university professor, who is himself dragged into a global conspiracy. Humorously, at one point, they use a 5-letter password (which just happens to the female cryptologist’s name, just like in the Da Vinci Code). And like every Dan Brown book, this book also happens to begin with someone dying, who, as the holder of a secret, tries to reveal his secret before he dies.

The more unfortunate thing was the portrayal of mathematics and computer science in Digital Fortress. Terrifying, really.

I watched Neon Genesis Evangelion this summer again, and I’m watching El Hazard now. I am extremely tempted to purchase Mysterious Cities of Gold DVD’s—does anyone else remember how awesome that was?

My cat Tasha is beautiful, and I will miss her while I am in Berkeley.

I am extraordinarily excited by the possibility that Sufjan Stevens might, in his epic quest to author a musical tribute for all 50 states, choose Minnesota next. Perhaps I am swayed by the fact that I am listening to Sufjan Stevens’ The Avalanche, and realizing again that I rather love him.

And I spend quite a bit of time brushing my teeth everyday, but I rather rarely discuss toothbrushing technique, or, for instance, how I learned to brush my teeth.

My Forget Me Not plug-in for Safari was reviewed on MacWorld!

• MacWorld
• Apple Matters
• MacUser

It’s great to read the comments and find out what users wish were different: a lot of people don’t just want to Unclose Window but also Unclose Tab.

For me, I really would have liked to have Unclose Window be underneath the Edit menu, but because the undo hierarchy is linked to the window (i.e., when you switch windows, the possible things you can undo changes) it isn’t possible to undo the very destruction of the window itself.

The whole idea of “undoing” something is very amusing, especially the modern sense; the old sense of “undoing” something by destroying it is quite dissimilar from the idea of restoring to a previous state.

In August, two of my friends from college have died: Daniel Bartlett and Michelle Knapp. I’m not sure what else I can say; I remember them so clearly…